들어가기에 앞서
이 포스트는 Part 04에 해당되며, Adam이 왜 잘 되는지 그리고 Convex 환경에서 Adam의 수렴성을 수학적으로 알아보겠습니다. 이 시리즈에 대한정보는 다음과 같습니다.
- Part 01: Adam의 기본적인 원리 파악, 코드 구현 및 장단점 분석
- Part 02: Adam 논문 분석
- Part 03: PyTorch로 코드 구현
- Part 04: Adam이 왜 잘 되는지 수학적으로 증명 (Convergence 증명)
Adam의 논문은 아래 사이트에서 확인할 수 있으며, 반드시 옆에 띄우고, 12 page의 APPENDIX 부분을 같이 보시기 바랍니다.
Adam: A Method for Stochastic Optimization
옵티마이저가 잘 동작한다는 것을 어떻게 증명하지?
어떤 잘 정의된 문제가 주어지고, 그 문제를 해결하는 컴퓨터 알고리즘에는 Complexity라는 개념이 들어갑니다. Complexity는 그 알고리즘이 얼마다 빠르게 문제를 해결할 수 있는지에 관한 지표입니다. 인공지능의 옵티마이저도 일종의 알고리즘이기 때문에 Complexity와 유사한 개념의 알고리즘 성능지표가 있습니다. 바로 Convergence rate입니다. 이 Convergence rate는 보통 주어진 convex loss 환경에서 알고리즘이 얼마나 빠르게 loss를 0으로 만드는지에 관한 지표입니다. 하지만 인공지능과 같은 환경에서는 loss 자체보다는 다음과 같은 regret을 잘 바운딩하는 것을 목표로 하고 있습니다. 이러한 regret을 기반으로 convergence rate를 보이는 환경을 Online Gradient Descent라고 합니다. 여리서 online이라는 뜻은 입력 데이터가 실시간으로 들어온다는 의미입니다. (우리가 아직 보지 못한 입력 데이터가)

Adam 같은 옵티마이저 뿐만 아니라 현대의 대부분의 옵티마이저는 regret인 R(T)를 어떤 값으로 바운딩하는 것을 목표로 하고 있습니다. 일단 결과적으로 Adam은 다음과 같은 복잡한 수식에 의거해 R(T)가 바운딩됩니다. 즉, convex 환경에서 loss가 오른쪽 항보다는 무조건 작거나 같다는 의미죠. 논문

위의 수식이 상당히 복잡해 보이지만, Adam 알고리즘으로부터 위의 수식을 유도해 볼 것입니다. 그 전에 Convex가 뭐고, convex의 특징이 뭔지는 알아야겠죠?
Convex란?
쉽게 말하면 어떤 함수 f(t)가 U자 모양이라는 의미입니다. 측 global optima가 존재하는 함수입니다. 또한 수학적으로 그래프의 특징을 설명하는 용어입니다. 수학적인 특징이니, 수식으로 정의할 수 있겠죠? 하지만 우리는 convex의 정의보다는 convex의 특징만 알아볼 것입니다. 우리가 알아야 할 Convex의 특징은 다음과 같습니다.


특징 01에서 f는 loss이며, y와 x는 loss 함수 위의 어떤 임의의 점입니다. 인공지능으로 따지면 가중치 혹인 파라미터에 해당되죠. g는 x에서의 기울기입니다. 여기서 f의 값은 스칼라 값이며, x, y, g는 n 차원의 벡터입니다. 즉, 위의 수식에서 인공지능의 파라미터는 정확히 n개라는 의미죠. Convex에는 여러 특징이 있지만, 우리에게는 위의 특징만 있으면 됩니다. 위의 수식을 조금 변형하면 우리가 필요한 regret과 관련된 수식이 나옵니다. y에는 x*, x에는 xt를 넣었습니다.

위의 마지막 식에 대해 t를 1부터 T까지 더하면 regret R이 나오게 됩니다. x*는 global optima입니다. 마침 gT와 관련된 식으로 upper 바운딩(상한)되어 있네요. 우리가 할 일은 Adam의 수식을 변형하여 gT 식에 Adam의 수식을 넣는 작업입니다. 그러면 이제 Adam을 봐야겠죠? 그 전에 왜 Convex를 가정하는지 보겠습니다.
왜 Convex 함수에서 증명하지?
이유는 간단합니다. 가장 간단한 convex 환경에서 일단 잘 동작이 되어야 하기 때문입니다. loss function의 가장 간단한 형태는 convex 형태이며, 이 간단한 형태에서 잘 작동 되어야 다른 non-convex function을 논할 수 있기 때문입니다. 또한 non-convex function은 수많은 부분 convex로 이뤄져 있기 때문에, 많은 옵티마이저 논문들이 일단 convex 환경에서 가중치가 global optima에 수렴한다는 것을 증명합니다. 정리하면 아래와 같이 말할 수 있습니다.
일단 가장 간단한 환경(conex)에서 잘 동작함이 보장되어야 하기 때문.
Adam의 수식을 변형하자
일단 Adam의 수식부터 알아보자
Adam

증명 유도
위의 수식에서 우리는 gT(x_t - x*) 식을 유도할 것입니다. 하지만 gT(x_t - x*)와 위의 수식은 벡터에 관한 수식이기 때문에 우리는 일단 벡터의 각 원소의 계산 후, 이를 취합함여 벡터 연산으로 표현할 것입니다. 따라서 다음과 같은 관계를 통해 일단 원소부터 계산합니다. n은 벡터의 길이입니다.
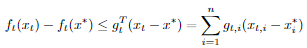
이제 우리는 Adam의 수식을 벡터 원소에 대한 수식으로 표현하고, 위의 g_t,i와 관련된 수식을 유도하면 됩니다. 다음과 같이요. 간단한 증명을 위해 epsilon e는 0으로 가정합니다.

첫 번째 등호는 벡터 기반의 Adam의 수식을 원소 기반의 표현으로 바꾼 것입니다. 두 번째 수식은 양변에 x*를 빼고 제곱한 것입니다. 세 번째 등호는 제곱을 전개한 것입니다. 네 번째 수식은 Adam 수식에 의거하여 우변 두 번째 항을 m_{t-1}과 관련된 수식으로 변환한 것입니다.
수식이 많이 길어졌지만, 드디어 우리가 원하던 g_t,i와 관련된 수식이 우변 두 번째 항에 나왔습니다. 따라서 g_t,i로 정리하겠습니다.

좌변을 regret을 계산할 때 필요한 g_t,i로 표현했습니다. 우변 두 번째 항은 Young's inequality를 적용시키기 위해 위와 같은 형태로 적었습니다. Young's inequality를 적용하기 위해 우변 두 번째 항의 순서를 바꾸겠습니다.

이게 위의 수식 우변의 두 번째 항에 Young's inequality(영 부등식)을 적용시키겠습니다. 쉬운 유도를 위해 다음과 같이 명시적으로 표현하겠습니다.

추가로 우변에 첫 번째 항과 세 번째 항을 바운딩하기 위해 다음과 같은 성질을 이용합니다. beta_1이 1보다 작기 때문에 아래의 수식은 유효합니다.

자 이제 g_t,i를 바운딩하겠습니다. 일단 첫 번째 항과 세 번째 항을 바운딩한 후, 두 번째 항을 바운딩하겠습니다.

첫 번째 부등식은 beta 바운딩을 이용하여 첫 번째 항과 세 번째 항을 바운딩한 것입니다. 두 번째 부등식은 Young's inequality를 시용하여 바운딩함과 동시에 세 번째 항의 제곱을 풀어줬습니다. 우리가 이제 할 것은 마지막 부등식의 세 번째 항을 바운딩하는 것입니다. a_t * hat(m ^ 2)/ sqrt(hat v)를 바운딩하겠다는 의미입니다. Adam은 여기서 a_t를 1/sqrt(t)로 설정하고 바운딩을 진행합니다. 다음과 같이요.

차근차근 어떤 원리로 바운딩이 되었는지 알아보겠습니다. 일단 첫 번째 등호는 단순히 시그마를 T-1과 T로 분할한 것입니다. 그 뒤에 m과 v를 g에 관한 수식으로 바꾼 것이죠. Adam 논문을 보신 분들이라면 m이 어떻게 g와 beta1만으로 그리고 v가 어떻게 g와 beta2만으로 표현되는지 아실 겁니다.
- 첫 번째 부등호는 convex 함수의 특징을 이용한 것입니다. 부등식의 두 번째 항의 분자는 x^2의 형태이고, x^2는 convex 함수이기 때문에 초반에 언급한 "convex 특징 02"을 변형하면 첫 번째 부등호가 성립하게 됩니다.
- 두 번째 부등호는 concave의 특징을 이용한 것입니다. concave 특징은 "convex 특징 02"에서 부등호의 방향만 바뀐 것입니다. 부등로의 두 번째 항의 분모는 sqrt(x)의 형태이고, 이 형태는 concave이기 때문에 "convex 특징 02"에서 부등호 방향만을 바꾸고, 시그마를 통일시키면 두 번째 부등호가 나옵니다.
- 세 번째 부등호는 다음과 같은 Adam의 가정에서 도출됩니다. ||gk,i||2는 L2-norm의 정의에 의거 나온 것입니다.

- 마지막 부등호는 beta1과 beta2에 관한 수식을 r로 표현하고, 적절한 산술적인 부등호 계산을 통해 도출된 것입니다.
이제 마지막 식 두 번째 항을 모든 T에 대해 summation을 취하면 다음과 같은 수식이 나오게 됩니다.

r은 1보다 작기 때문에, 다음의 부등식이 성립됩니다.


이제 마지막으로 논문의 Lemma 10.3을 적용하면 다음과 같이 비교적 간단한 형태로 바운딩이 가능합니다.

자 이게 위의 "간단한 바운딩"을 "더더욱 어려운 수식"에 대입하면 다음과 같은 regret을 바운딩하는 길고 긴 수식이 나옵니다. 물론 어느정도 정렬을 했습니다. 아래의 수식에서 sum i=1 d라는 연산이 있는 이유는 벡터 연산과 벡터 원소 연산의 관계를 연산하기 위함입니다. 제가 위에서 설명을 했죠? 참고로 여기서 theta는 위에서 계속 사용한 x와 동일합니다.

그 다음으로 다음과 같은 가정이 필요합니다. 일반적으로 optimizer의 가정은 아래와 유사합니다. 즉, 공통적으로 갖는 가정이죠.

좌측 부등식은 loss function 어느 위의 한 점 theta n에서 global minima까지의 거리는 D 이하이다. 우측 부등식은 loss function 위의 어떠한 두 점 사이의 거리 최대값이 D_inf 이하이다를 의미합니다. 이 수식은 "R 바운딩" 수식에 도입하면 다음과 같은 부등식을 얻을 수 있습니다.

마지막으로 산술 계산으로 마지막 항 다음과 같이 바운딩 합니다. 여기서 beta1의 가정이 들어갑니다.

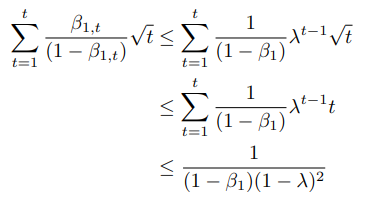
이제 산술계산 바운딩 수식을 대입하면 다음과 같은 최종 수식이 나오게 됩니다.

마치며
여기까지 Convex 환경에서 Adam이 잘 동작하는지 수식적으로 확인해 보았습니다. 사실 위의 증명에서 제가 쓴 부분과 논문에 나온 부분들이 섞여 있기 때문에 표기법이 잘 안 맞을 수 있습니다. 하지만, 전체적인 흐름은 논문과 일치하며, 논문에서 이 포스트의 내용을 찾고 싶으시면, 논문의 12 page APPENDIX 부분을 정독하시면 됩니다.
위의 수식들은 모두 논문의 APPENDIX에서 가져온 수식들입니다. Adam을 소개한 논문에서는 위의 수식에 문제가 없는 것처럼 보였지만, 사실은 그 후에 나온 AMSGrad 논문에서 Adam의 증명에 사용된 가정이 틀렸고, Adam이 동작하지 못하는 convex 함수를 보이기도 했죠. 하지만, 우리가 사용하는 인공지능의 loss function은 non-convex하기 때문에 보통은 Adam을 사용해도 문제는 없습니다.



